FraBoMat,
Concepts for analysing, joining and reading Biblical manuscripts and Genizah fragments
(Konzepte
zum automatischen Lesen und Identifizieren von Handschriften aus
Geniza-Funden und Bibliotheken).
31.3.2021, updated 6.2.2022
In
September 2020 I have done some programming for computer based
manuscript analysis in the field of hebrew studies. I am working on
manuscripts from the Cairo genizah(s) since years and enjoyed the new
possibilities offered by the Friedberg
Genizah Project (FGP) .
This project offers analysis of manuscripts resulting in the numbers
of written lines on a page of an Hebrew fragment and the hight of the
lines and the distances between the lines etc.
Sometimes I would
like to overwrite the data coming from the FGP with my own. This
desire resulted in starting some experiments in programming with
NN-libraries like tensorflow and PyTorch and Reforcement Learning
mechanisms in about 2018. Because I worked 8 years in computer
business mostly as programmer in the first decade of this millenium I
never lost interest in the field, but prefered to work again in the
area of theology: Since 2009 I am a religious teacher in schools in
Austria and Germany and I like it. Programming is leisure time ...
and fun. And because of my previous work with FGP resulted since 2014
in some finds of new manuscripts of a rhymed Hebrew paraphrase on an
Hebrew original text of Ben Sira I am motivated to continue in this
mixture of manuscripts studies and computer programming. The
understanding how machine learning works helped me a lot in using the
FGP system and the possibilities for queries in the databeses it
offers. Now I would like to program my own system which could be used on any image of Biblical manuscripts or Genizah fragments.
Crazy? Yes, but it was also crazy to find hebrew manuscripts the exegetical community slept about for decades ;-)
Here I can show first results of my own programming.
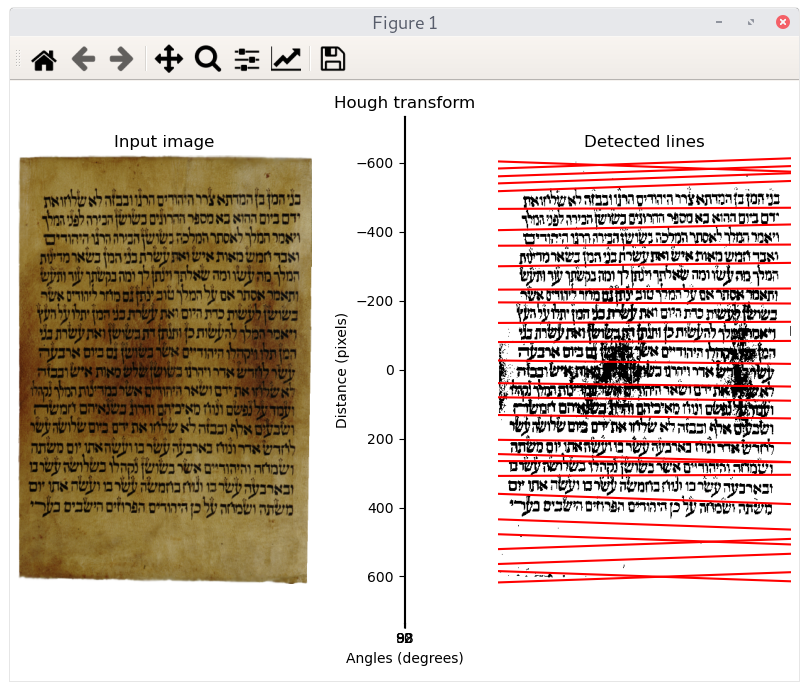
 The following image shows the classic approach using
crosscorrelation – and it was very effective from
the beginning. This heuristic allows the fast finding of almost 98 %
of the letters. Using the neural network heuristic for hebrew letters
(see at the bottom) the wrong indentifications can mostly be
suspended.
The following image shows the classic approach using
crosscorrelation – and it was very effective from
the beginning. This heuristic allows the fast finding of almost 98 %
of the letters. Using the neural network heuristic for hebrew letters
(see at the bottom) the wrong indentifications can mostly be
suspended.
The area of writing on the manuscript can be found by using
complex hull mechanisms after cleaning of the manuscript of the
darkened areas by some filters like the otsu-filter and similar
mechanisms:

When looking on this
convex hull analysis of the page of an Esther scroll fragment you
might be surprised like me about the clear visible movement of the
edges left and right. I had seen that the writer had a tendence to
write more on the left side at the bottom from line to line – but I
did not see this at the right side before the marking by the hull
mechanism. This small drifting in the writing practice can help
identify writers together width the hight of the letters, the spacing
of letters, the line spacing and the letter chart of letters of any
writer (like a fingerprint of the writer).
Some other
mechanisms like mathematical morphological methods on whole pages
help do find the writing
area.
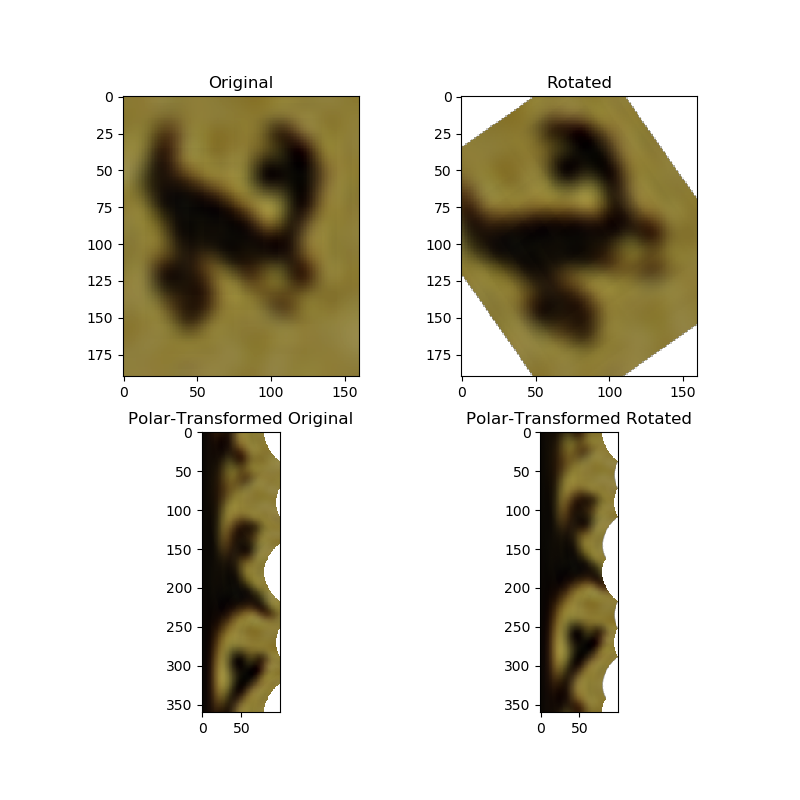
One technique I
thought about and developped on my own but found it programmed also
in skimage is polar rotation of letters and analysing the rotation
accordingly. You can see an hebrew letter aleph in original (scaled
up from a small version in gimp to make it blur) and a polar
transform of the original. At the
right you see the letter rotated by a known degree and the polar
transform. It is mathematically clear that the result ist just a
shift by the amount of the degrees as you can see comparing the
polar-transformed images. The program can identify the rotation with
a precision of 1-3°.

Another technique I
use is the dct (discret cosinus transform) which analyses the
frequencies of any line and column of the image and results in an
frequence spectrum of the image. By masking out some (high)
frequencies in both directions and reconstruct the image some
disturbing small artifacts in the images can be reduced. The result
above shows the reconsctructed image after using a high pass filter
and another technique which is called mathematical morphology (using
dilation, erosion and mixing the both closing and opening). This
helps in determining written areas (I have overpressed here to make
the effect more clearly visible).
The next step in my
computer based manuscript study has been based on producing a dataset
of hebrew letters. The easiest way was to make a synthetic dataset of
fonts – what you can write you also can read. What a computer can
write it also can read – when trained on it.
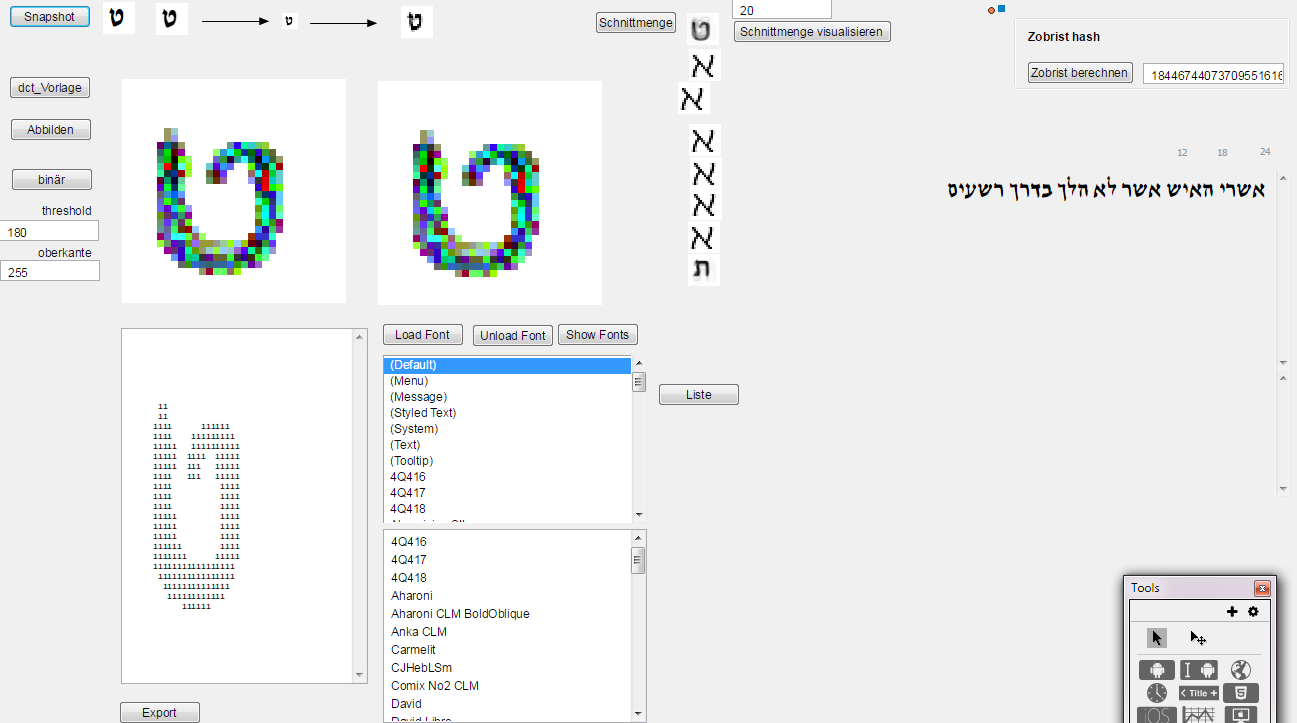 First
I produced my own synthetic hebrew dataset. This is necessary for
supervised learning: You need the pixel representation of a glyph (=
the visual representation of a character) and the label for it in a
database. Then a neural network in a machine learning process can go
through thousands of items in the labelled database and optimize its
parameters to identify characters from pixel glyphs. For avoiding
analysing hundreds of manuscripts (as many actual initiatives even on
academic level do with thousands of hours of working of volunteers
identifiing glyphs on manuscripts) I had to produce a synthetic
datasets of very different hebrew scripts with correct labels in a
database.
First
I produced my own synthetic hebrew dataset. This is necessary for
supervised learning: You need the pixel representation of a glyph (=
the visual representation of a character) and the label for it in a
database. Then a neural network in a machine learning process can go
through thousands of items in the labelled database and optimize its
parameters to identify characters from pixel glyphs. For avoiding
analysing hundreds of manuscripts (as many actual initiatives even on
academic level do with thousands of hours of working of volunteers
identifiing glyphs on manuscripts) I had to produce a synthetic
datasets of very different hebrew scripts with correct labels in a
database.
The basic idea upon which this undertaking rests is
that any computer does nowadays understand fonts because
he can write it out of installed fonts based on the unicode standard.
א
(Aleph) has its own unicode number and
can be written in most modern unicode fonts. When I started my
internet activities in 1994 more than 25 years ago this was not
standard and just started to spread on the internet. Now it is
standard and the young people do not even thing about the problems of
the dinosaurs. Therefore I installed all hebrew fonts I could find
and wrote programs to convert all hebrew glyphs into a database.

One
program is written in python and works but I did not use it actually
because I preferred my old visually oriented programming environment
livecode. The result looks like this:
The result is a database of hebrew glyphs in the format 32x32
pixel (=1024 byte with grey values 0 to 255) and the correct label
with the character number and the name of the font.
In a first attempt the dataset consists out of 13000 glyphs. I
prgrammed a technique to mix around 20 glyphs from different random
glyphs which results in glyphs similar to scanned glyphs from
manuscripts. But mathematically it might be just a small progress to
offer the neural networks thousands of this generated and mixed
glyphs. The adapted parameters reading all the buildt in glyphs
should do the same for the mixed glyphs also.
For the neural network I avoided cnn (convolution) but
experimented with small sequential nets in python, tensorflow and
keras - and it worked on my 10 year old windows notebook with 4 GB
RAM. I had installed conda on this win7 notebook (without a graphic
card usable by cuda, but with one of the first core i5 processors)
and Pycharm. The first attempt resulted in 95 %accuracy after a run
of 30 minutes. The following model with one hiffen layer more (the
512 nodes layer at level 2 instead going to 256) resulted in 97%
accuracy and run about 40 minutes for the 300 epochs (300 times going
through the whole dataset and adapting the parameters for reading the
glyphs). That means only 30 errors in correct identification of all
glyphs out of a set of 1000 different pixel representations. The
graphic above shows 20x50 = 1000 glyphs of hebrew characters in
different fonts and statistically 30 from them are misinterpreted.
That is near perfect and enought for me ;-).
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(512,
input_shape=(1024,),activation=tf.nn.relu),
#tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(256, activation=tf.nn.relu),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
#tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation=tf.nn.relu),
#tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(28, activation=tf.nn.softmax)
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
Epoch 300/300
64/9999 [..............................] 64/9999
[..............................] - ETA: 4s - loss: 0.0424 - acc:
0.9844
192/9999 [..............................] 192/9999
[..............................] - ETA: 4s - loss: 0.0363 - acc:
0.9792
320/9999 [..............................] 320/9999
[..............................] - ETA: 4s - loss: 0.0278 - acc:
0.9844
448/9999 [>.............................] 448/9999
[>.............................] - ETA: 4s - loss: 0.0316 - acc:
0.9821
576/9999 [>.............................] 576/9999
[>.............................] - ETA: 4s - loss: 0.0308 - acc:
0.9826
704/9999 [=>............................] 704/9999
[=>............................] - ETA: 4s - loss: 0.0254 - acc:
0.9858
832/9999 [=>............................] 832/9999
[=>............................] - ETA: 4s - loss: 0.0282 - acc:
0.9844
960/9999 [=>............................] 960/9999
[=>............................] - ETA: 3s - loss: 0.0260 - acc:
0.9865
1088/9999 [==>...........................]1088/9999
[==>...........................] - ETA: 3s - loss: 0.0270 - acc:
0.9871
1216/9999 [==>...........................]1216/9999
[==>...........................] - ETA: 3s - loss: 0.0251 - acc:
0.9885
1344/9999 [===>..........................]1344/9999
[===>..........................] - ETA: 3s - loss: 0.0280 - acc:
0.9881
1472/9999 [===>..........................]1472/9999
[===>..........................] - ETA: 3s - loss: 0.0267 - acc:
0.9891
1600/9999 [===>..........................]1600/9999
[===>..........................] - ETA: 3s - loss: 0.0268 - acc:
0.9888
...
8768/9999 [=========================>....]8768/9999
[=========================>....] - ETA: 0s - loss: 0.0452 - acc:
0.9841
8896/9999 [=========================>....]8896/9999
[=========================>....] - ETA: 0s - loss: 0.0459 - acc:
0.9838
9024/9999 [==========================>...]9024/9999
[==========================>...] - ETA: 0s - loss: 0.0470 - acc:
0.9836
9152/9999 [==========================>...]9152/9999
[==========================>...] - ETA: 0s - loss: 0.0469 - acc:
0.9836
9280/9999 [==========================>...]9280/9999
[==========================>...] - ETA: 0s - loss: 0.0484 - acc:
0.9834
9408/9999 [===========================>..]9408/9999
[===========================>..] - ETA: 0s - loss: 0.0493 - acc:
0.9832
9536/9999 [===========================>..]9536/9999
[===========================>..] - ETA: 0s - loss: 0.0490 - acc:
0.9833
9664/9999 [===========================>..]9664/9999
[===========================>..] - ETA: 0s - loss: 0.0485 - acc:
0.9835
9792/9999 [============================>.]9792/9999
[============================>.] - ETA: 0s - loss: 0.0490 - acc:
0.9834
9920/9999 [============================>.]9920/9999
[============================>.] - ETA: 0s - loss: 0.0497 - acc:
0.9831
9999/9999 [==============================]9999/9999
[==============================] - 4s 436us/step - loss: 0.0496 -
acc: 0.9830
64/2765 [..............................] 64/2765
[..............................] - ETA: 1s
576/2765 [=====>........................] 576/2765
[=====>........................] - ETA: 0s
1088/2765 [==========>...................]1088/2765
[==========>...................] - ETA: 0s
1600/2765 [================>.............]1600/2765
[================>.............] - ETA: 0s
2112/2765 [=====================>........]2112/2765
[=====================>........] - ETA: 0s
2624/2765 [===========================>..]2624/2765
[===========================>..] - ETA: 0s
2765/2765 [==============================]2765/2765
[==============================] - 0s 112us/step
test loss, test acc: [0.07396609171457293, 0.9775768535262206]
A second concept based on a neural network including normalized
Image moments and Hu-moments got 99% accuracy on the testset
(training on 9999 items of the 12764 item testset, testset the rest
consisting of 2765 items).
A new approach was a Variational Autoencoder applied on the
FraBoMat hebrew letter testset.
The results with different network topologies:
a)
b)
c)

 The following image shows the classic approach using
crosscorrelation – and it was very effective from
the beginning. This heuristic allows the fast finding of almost 98 %
of the letters. Using the neural network heuristic for hebrew letters
(see at the bottom) the wrong indentifications can mostly be
suspended.
The following image shows the classic approach using
crosscorrelation – and it was very effective from
the beginning. This heuristic allows the fast finding of almost 98 %
of the letters. Using the neural network heuristic for hebrew letters
(see at the bottom) the wrong indentifications can mostly be
suspended.


 First
I produced my own synthetic hebrew dataset. This is necessary for
supervised learning: You need the pixel representation of a glyph (=
the visual representation of a character) and the label for it in a
database. Then a neural network in a machine learning process can go
through thousands of items in the labelled database and optimize its
parameters to identify characters from pixel glyphs. For avoiding
analysing hundreds of manuscripts (as many actual initiatives even on
academic level do with thousands of hours of working of volunteers
identifiing glyphs on manuscripts) I had to produce a synthetic
datasets of very different hebrew scripts with correct labels in a
database.
First
I produced my own synthetic hebrew dataset. This is necessary for
supervised learning: You need the pixel representation of a glyph (=
the visual representation of a character) and the label for it in a
database. Then a neural network in a machine learning process can go
through thousands of items in the labelled database and optimize its
parameters to identify characters from pixel glyphs. For avoiding
analysing hundreds of manuscripts (as many actual initiatives even on
academic level do with thousands of hours of working of volunteers
identifiing glyphs on manuscripts) I had to produce a synthetic
datasets of very different hebrew scripts with correct labels in a
database.




